Repetitive Nearest Neighbour Algorithm
- Pick a vertex and apply the Nearest Neighbour Algorithm
with the vertex you picked as the starting vertex.
- Repeat the algorithm (Nearest Neighbour Algorithm) for each vertex of the graph.
- Pick the best of all the hamilton circuits you got on
Steps 1 and 2.
- Rewrite the solution by using the home vertex as the starting
point.
Nearest Neighbor Circuit from A
It starts by going from A to D, from D it goes to E, from E to C from
C to B and then finaly from B to A. Below the circuit is marked with
the boldface edges. Calculate the weight of this circuit.
 |
Nearest Neighbor Circuit from B
It starts at B. From there it goes to C, from C it goes to E, from E
to A from A to D and then finaly from D to B. Below the circuit is
marked with the boldface edges. Calculate the weight of this
circuit.
 |
Nearest Neighbor Circuit from C
It starts at C, from C it goes to E, from E to A, from A it goes to D,
from D to B and then finaly from B to C. Below the circuit
is marked with the boldface edges. Calculate the weight of this
circuit.
 |
Nearest Neighbor Circuit from D
It starts by going from D to A, from A it goes to C, from C to E from
E to B and then finaly from B to D. Below the circuit is marked with
the boldface edges. Calculate the weight of this circuit.
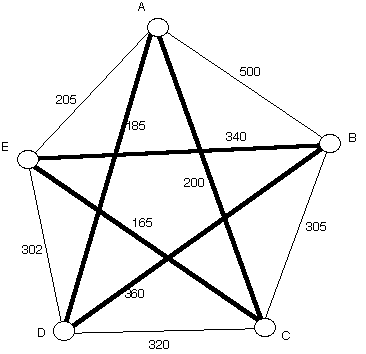 |
Nearest Neighbor Circuit from E
It starts at E, then it heads to C, from C it goes to A, from A to D from
D to B and then finaly from B to E. Below the circuit is marked with
the boldface edges. Calculate the weight of this circuit.
 |
Thus, the best choice out of these five answers is the one that starts from B
or C. But what can we do when our home vertex is a vertex other than
these two vertecies, say A? No worry, take the B-C-E-A-D-B
circuit and rewrite it starting at A to get A-E-C-B-D-A. It is
the same circuit with the same weight. This weight is 1220.
Coincidentally this is also the optimal soultion. Note that the
Repetitive nearest neighbour algorithm is efficient but not
necessarily optimal. In this particular example, however, it
managed to get the optimal solution as well.
The Repetitive Nearest Neighbor Circuit
 |