Chapter 5 Practice Problems

Part I (Multiple Choice)


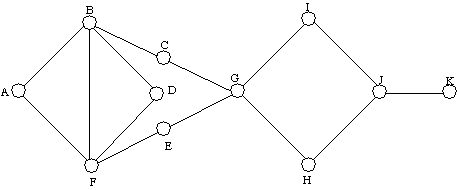Figure 1
  1. Which of the following edges is a bridge of the graph in Figure 1

    1. BC
    2. GH
    3. IJ
    4. JK
    5. None of these

  2. How many vertices does the graph in Figure 1 have?

    1. 10
    2. 12
    3. 11
    4. 9
    5. None of these

  3. How many edges does the graph in Figure 1 have?

    1. 10
    2. 14
    3. 13
    4. 12
    5. None of these

  4. The graph in Figure 1 is eulerian (has an eulerian circuit).

    1. True
    2. False

  5. The graph Figure 1 has an eulerian path.

    1. True
    2. False

  6. Which of the following is not a circuit in the graph in Figure 1?

    1. A, B, F, A
    2. A, B, D, F, A
    3. A, B, C, D, E, F, A
    4. G, I, J, H, G
    5. None of these

  7. A graph with 7 vertices has an eulerian path but not an eulerian circuit. The graph must have

    1. 7 vertices of even degree
    2. 5 vertices of odd degree and 2 vertices of even degree
    3. 2 vertices of odd degree and 5 vertices of even degree
    4. 2 vertices of even degree and 4 vertices of odd degree, and one isolated vertex
    5. None of the above

  8. A graph has 8 vertices and 13 edges; the seven vertices have the following degrees:
    2, 5, 4, 2, 3, 5, 2. Find the degree of the remaining vertex.

    1. 1
    2. 2
    3. 3
    4. 5
    5. None of the above

    Part II: Show all your work for this part.

  9. How Does Fleury's algorithm work?

  10. State, in your own words, Euler's theorems.

  11. Give at least five applications that Euler's theorem can be used.

  12. Find an optimal eulerization for the graph shown in Figure 2. Make sure to mark your deadhead edges.

    Figure 2

  13. Find, using Fleury's algorithm, an euler circuit for the eulerized graph of Figure 2 you did in Problem # 12.